RESOLUÇÃO DO EXAME DE ADMISSÃO DE QUÍMICA DA UP - 2020
1. São dados
três átomos genéricos A, B e C. O átomo A tem número atómico 70 e número de
massa 160. O átomo C tem 94 neutrões, sendo isótopo de A. O átomo B é isóbaro
de C e isótono de A. O número de electrões do átomo B é:
A 160
B 70
C 74
D 164
RESOLUÇÃO
Para resolvermos esta questão temos que ter a noção acerca das Semelhanças Atómicas e das Características dos Átomos.
Primeiramente recordemo-nos dos seguintes conceitos:
Isótopos - são átomos do mesmo elemento químico (com mesmo número atómico) mas com diferente número de massa;
Isóbaros - são átomos de elementos químicos diferentes (ou seja, com diferente número atómico (Z) mas com o mesmo número de massa (A).
Isótonos - são átomos de elementos químicos diferentes (ou seja, com diferente número atómico (Z) e diferente número de massa (A) mas que têm igual número de neutrões (N).
Como o átomo C é isótopo de A significa que têm o mesmo número atómico (Z) e é por isso que o número atómico de C é 70. Como temos dados suficientes podemos calcular o número de neutrões do átomo A e o número de massa do átomo C:
|
Átomo
A |
Átomo
C |
|
Número atómico (Z) = 70 |
Número de neutrões (N) = 94 |
|
Número de massa (A) = 160 |
Número atómico (Z) = 70 |
|
Número de neutrões (N) A = Z + N 160 = 70 + N N = 160 – 70 N = 90 |
Número de massa (A) A = Z + N A = 70 + 94 A = 164 |
O átomo B é isóbaro de C, logo “B” e “C” têm o mesmo número de massa. E o átomo B é isótono de A logo, “A” e “B” têm o mesmo número de neutrões.
Assim, para o átomo B temos o número de massa (A) e o número de neutrões (N) o que significa que podemos calcular o número atómico (Z) do átomo B:
|
Átomo
B |
|
|
Número de massa: 164 |
Número atómico (Z) |
|
Número de neutrões: 90 |
A = Z + N 164 = Z + 90 Z = 164 – 90 Z = 74 |
Como trata-se de um átomo neutro, significa que o número de atómico (que corresponde ao número de protões existentes no núcleo do átomo) é igual ao número de electrões: Z = p+ = e-:
Portanto, o número de electrões do átomo B é 74.
Resposta: alternativa: C
2. Dados os
seguintes átomos hipotéticos 90X233 , aYb
e cZd. Sabendo que o átomo Z tem 144 neutrões, é isótopo
de X e isóbaro de Y e que o átomo Y é isótono de X; então o átomo Y deve ter:
A 90 protões
B 91 protões
C 143 protões
D 42 protões
RESOLUÇÃO
Para resolvermos este exercício temos que seguir o mesmo raciocínio que usamos para resolver o exercício número 1.
O átomo Z é isótopo de X, o que significa que “Z” e “X” têm o mesmo número atómico. E este mesmo átomo Z é isóbaro de Y o que significa que o átomo “Z” e “Y” têm o mesmo número de massa. O átomo Y é isótono de X, o que significa que “Y” e “X” têm o mesmo número de neutrões (N).
Notem que temos para o átomo X o número de massa (A) e o número atómico (Z), logo podemos calcular o número de neutrões do átomo X e que será o mesmo valor para o átomo Y dado que X e Y são isótonos:
|
Átomo
X |
Átomo
Z |
Átomo
Y |
|
Número atómico (Z) = 90 |
Número atómico (Z) = 90 |
Número de massa (A) = 234 |
|
Número de massa (A) = 233 |
Número de neutrões (N) = 144 |
Número de neutrões (N) = 144 |
|
Número de massa (A) A = Z + N 233 = 90 + N N = 233 – 90 N = 143 |
Número de massa (A) A = Z + N A = 90 + 144 A = 234 |
Número atómico (Z) A = Z + N 234 = Z + 144 Z = 234 – 144 Z = 90 |
Resposta: alternativa: A
3. Na explicação
dos aspectos contraditórios que o modelo de Rutherford apresentava, Bohr tomou
como base a:
A Estrutura do
núcleo do átomo
B Teoria do
electromagnetismo
C Teoria da
relatividade
D Quantização
de energia
RESOLUÇÃO
Resposta: alternativa: D
4.
Considerem-se dois compostos E e F, sendo o primeiro molecular e o segundo
iónico. Pode-se afirmar que:
A os dois
quando fundidos, sempre conduzem a corrente eléctrica;
B os dois
quando em solução aquosa, sempre conduzem a corrente eléctrica;
C somente E
pode conduzir a electricidade, quando ambos estão em solução;
D no composto
F, podem ocorrer ligações covalentes entre os átomos.
RESOLUÇÃO
PROPRIEDADES DAS SUBSTÂNCIAS IÓNICAS
⦁ São sólidos
duros e quebradiços à temperatura ambiente;
⦁ Possuem altos
pontos de fusão e ebulição, pois é necessário uma grande quantidade de energia
para quebrar a atracção electrostática entre os iões (ligação);
⦁ Conduzem corrente
eléctrica em solução aquosa ou quando fundidos, pois os seus iões adquirem
mobilidade. São polares devido a formação efectiva de cargas opostas em sua
estrutura;
⦁ São bem solúveis
em água;
⦁ Devido à força de atracção
entre os iões, a estrutura é compacta, apresentando forma e volume constantes,
o que caracteriza o estado sólido.
⦁ Têm estrutura cristalina, isto
é, os iões se distribuem alternadamente, formando estruturas que são
denominadas retículos
cristalinos.
PROPRIEDADES DAS
SUBSTÂNCIAS COVALENTES
⦁ Têm pontos de fusão e ebulição baixos;
⦁ À temperatura ambiente podem apresentar-se nos estados sólido, líquido ou
gasoso;
⦁ Não são bons condutores
de corrente eléctrica. A excepção é a grafite que conduz corrente eléctrica.
Porém alguns ácidos fortes, por exemplo, em meio aquoso sofrem ionização
tornando a solução condutora de corrente eléctrica;
⦁ Em geral tem baixa
tenacidade, ou seja, baixa resistência mecânica, pois são muito quebradiços;
⦁ Têm baixa solubilidade em água.
Análise das alternativas:
A. INCORRECTA
Os compostos iónicos é que conduzem corrente eléctrica quando fundidos pois a solução resultante contém os iões que constituem estes compostos.
B. INCORRECTA
Os compostos iónicos é que conduzem corrente eléctrica em solução pois estes dissociam-se, ou seja, os iões que constituem estes compostos se separam o que causa a condutividade eléctrica.
C INCORRECTA
Somente F pode conduzir electricidade, quando ambos estão em solução aquosa, isto porque o composto F é um composto iónico e em meio aquoso, dissociam-se, ou seja, os iões que constituem estes compostos se separam o que causa a condutividade eléctrica. O E por ser molecular não forma no geral iões em solução aquosa por isso não pode conduzir electricidade.
D CORRECTA
Se F é um
composto iónico significa que estabelece ligações iónicas mas neste mesmo
composto pode-se estabelecer ligações covalentes. Note por exemplo, o NaCN,
este composto é formado por iões [Na]+ e [CΞN]-, por isso
é um composto iónico, porém, no mesmo
composto iónico ocorrem ligações covalentes, pois no ião cianeto, [CΞN]-
o Carbono e o Nitrogénio estabelecem entre si ligações covalentes. O composto E
por ser molecular estabelece ligações covalentes (ou moleculares).
Resposta: Alternativa: D
5. A
configuração electrónica do Enxofre (Z = 16), no estado fundamental, é:
A 1s2
2s2 2p6 3s2 3p2x
3p2y 3p0z
B 1s2
2s2 2p6 3s2 3p1x 3p2y
3p1z
C 1s2
2s2 2p6 3s2 3p2x 3p1y
3p1z
D 1s2
2s2 2p6 3s2 3p1x 3p1y
3p2z
RESOLUÇÃO
Para fazermos a distribuição electrónica deste átomo temos que seguir o Diagrama de Pauling, assim, a distribuição ou configuração electrónica deste átomo é:
1s2 2s2 2p6 3s2 3p4
No entanto,
sabe-se que o subnível “p” tem três (3) orbitais cuja disposição espacial é:
Assim, temos o Px , Py e o Pz . Representando em “caixinhas” (como é comum):
Agora voltando a configuração electrónica, vemos que no subnível p do nível 3 (3p) temos 4 electrões: 3p4. Então vamos distribuir estes electrões nestas “caixinhas” obedecendo a Regra de Hund ou Regra da Máxima Multiplicidade: “num mesmo subnível, de início, todos os orbitais devem receber o seu primeiro electrão, e só depois cada orbital irá receber o segundo”.
Notem que no orbital px temos 2 electrões, assim, a configuração electrónica do nosso átomo fica:
1s2 2s2
2p6 3s2 3p2x 3p1y
3p1z
Resposta: alternativa: C
6. Das
moléculas que se seguem: CO, C2H6, CO2, H2O,
NH3, as que apresentam ligações polares e apresentam carácter polar
são:
A Todas,
excepto C2H6
B Todas,
excepto CO e C2H6
C Todas,
excepto C2H6 e CO2
D Todas,
excepto C2H6 e NH3
RESOLUÇÃO
Apresentam ligações polares (existe diferença de electronegatividade entre os átomos): TODAS MOLÉCULAS.
Apresentam carácter polar (o momento dipolar (dipolo eléctrico) é diferente de zero): CO, H2O, e NH3, ou seja, todas excepto C2H6 e CO2.
Observem os exemplos:
Resposta: alternativa C
7. Que volume
de hidrogénio é necessário para a redução completa de 20 gramas de óxido de
cobre II?
A 5,6 litros
B 11,2 litros
C 4,48 litros
D 2,24 litros
RESOLUÇÃO
Equação da reacção:
CuO + H2 → Cu + H2O
Mr(CuO) = 63,54 + 16 = 79,54 g/mol ≅ 80 g/mol
Mr(H2) = 2 x 1 = 2 g/mol
Assim, 1 mol de Hidrogénio equivale a 2 g. Nas CNTP, 1 mol de um gás ocupa
22,4 L, logo:
1 mol ___________ 2 g ___________ 22,4 L
CuO + H2 → Cu + H2O
80 g____22,4 L
20 g _____ x
80 g · x = 20 g · 22,4 L
x = 20 g · 22,4 L / 80 g
x = 5,6 L
Resposta: alternativa A
8. O resíduo
da calcinação de uma mistura de carbonato de cálcio e hidróxido de cálcio pesou
3,164 g e o CO2 formado pesou 1,386 g. Calcule as percentagens dos
componentes (massas atómicas, em g/mole: Ca – 40; S – 32; C -12; O – 16).
A CaCO3
– 31,52%; Ca(OH)2 – 68,48%
B CaCO3
– 53,82%; Ca(OH)2 – 46,18%
C CaCO3
– 55,82%; Ca(OH)2 – 44,18%
D CaCO3
– 43,81%; Ca(OH)2 – 56,19%
RESOLUÇÃO
Massas molares: (A massa
atómica do Enxofre não é necessária neste exercício!)
Mr(CaCO3)
= 40 + 12 + 3 x 16 = 100 g /mol
Mr(CaO) = 40 +
16 = 56 g/mol
Mr[Ca(OH)2]
= 40 + 2 x 16 + 2 x 1 = 74 g/mol
Mr(CO2)
= 12 + 2 x 16 = 44 g/mol
PERCENTAGENS DE CaO
(ATENÇÃO A ESTA RESOLUÇÃO)
PERCENTAGENS DOS COMPONENTES (PEDIDO DO EXERCÍCIO)
Resposta: NÃO HÁ RESPOSTA
CORRECTA NESTA QUESTÃO!
9. Se se
dissolver 12,25 g de sacarose (C12H22O11) em
250 g de água pura, a concentração percentual em peso e molar serão
respectivamente, assumindo que a densidade da água é 1 g/cm3:
(massas atómicas, em g/mole: H = 1,01; C – 12,01; O – 16,00)
A 4,67%; 49
mole/l
B 4,90%; 1,43
x 10-4 mole/l
C 4,67%; 0,14
mole/l
D 4,90%; 0,14
mole/l
RESOLUÇÃO
Vamos tirar os dados
primeiro:
Massa do soluto (m1)
= 12,25 g
Massa do solvente (m2)
= 250 g
Como a densidade da água
é 1 g/cm3, tem-se:
1 g _______________ 1 cm3
250 g _______________ V
V = 250 cm3 =
0,25 L
10. Uma
solução preparada dissolvendo-se 0,25 mol de CaSO4 que se encontra
85% dissociado contém
A 3,1 ∙ 1023 partículas dispersas
B 2,78425 ∙ 1023 partículas dispersas
C 31 ∙ 1022 partículas dispersas
C 27,8425 ∙ 1022 partículas dispersas
RESOLUÇÃO
Dados
α = 85% = 0,85
n = 0,25 mol
CaSO4(aq) → Ca2+(aq) + SO42-
(aq)
Sabe-se que 1 mol
equivale a 6,02 · 1023 partículas
1 mol ______________ 6,02
· 1023 partículas
0,25 mol ___________ y
y = 1,505 · 1023
partículas
No entanto, vemos
na dissociação deste composto form-se 2 mol de iões, ou seja, 1 mol de CaSO4
origina dois 2 mol de iões e por causa disso temos que usar um factor de
correcção para obtermos o valor correcto do número de partículas e este factor
de correcção é denominado de Factor de
Correcção de Van’t Hoff (i) e é calculado usando-se a fórmula: i = 1 + α · (q – 1)
Onde:
⦁ i – factor de correccção de Van’t Hoff;
⦁ α – grau de dissociação ou ionização;
⦁ q – número de partículas dissociadas ou ionizadas
Calculando o “i”:
Note que na
dissociação forma-se 2 mol de iões:
CaSO4(aq) → Ca2+(aq) + SO42-
(aq)
1 mol + 1 mol = 2 mol
Logo: q = 2
i = 1 + α · (q – 1)
i = 1 + 0,85 · (2 – 1)
i = 1 + 0,85 · 1
i = 1,85
Agora é só
multiplicarmos o número de partículas que calculamos anteriormente pelo valor
do factor de correcção de Vam’t Hoff (i):
1,505 · 1023
x 1,85 = 2,78425 · 1023 partículas = 27,8425 · 1022
partículas.
Matematicamente
falando as alternativas B e D estão correctas. Mas considerando a notação
padrão da notação científica vamos escolher a alternativa B.
Resposta: alternativa: B
Por: Miguel Pascoal
GOSTOU DESTA RESOLUÇÃO E QUERIA TER ACESSO A VERSÃO COMPLETA? CLIQUE AQUI PARA COMPRAR A RESOLUÇÃO COMPLETA DESTE EXAME EM PDF OU CONTACTE 846767922.
PARA BAIXAR OS ENUNCIADOS DOS EXAMES DE ADMISSÃO DE QUÍMICA EM PDF clique aqui.
FIM







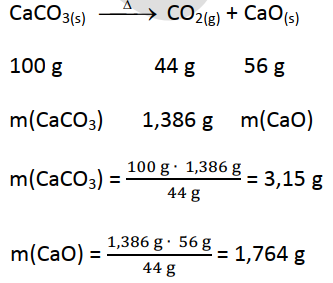










3 Comentários
Gostei muito
ResponderEliminarEstou a pedir me enviar o exames, por favor
ResponderEliminarEstou a pedir me enviar o exames, por favor
ResponderEliminar