PRÉ-QUÍMICO ___________________________________________________________________
Introdução
No artigo, Constantes de Equilíbrio, mostramos que
a constante de equilíbrio pode ser expressa em função das concentrações das
espécies químicas envolvidas no momento em que é atingido o equilíbrio.
No entanto, caso os
participantes da reacção (ou pelo menos um deles) encontrem-se no estado gasoso
ao invés de se expressar a constante de equilíbrio em função das concentrações
é comum a constante de equilíbrio ser expressa em termos de pressões parciais,
a qual é representada por Kp.
Contudo, não se quer
dizer que é errado expressar a constante de equilíbrio em função das
concentrações quando os participantes forem gases!
Pressão parcial
de um gás numa mistura gasosa
Pode ser entendida como a
pressão que um gás exerceria se estivesse sozinho dentro do recipiente de
volume V, à temperatura constante.
Constante de
quilíbrio termos de pressões parciais (Kp): relação entre Kc e Kp
Para que possamos
relacionar a pressão parcial de um gás com o volume da mistura, número de moles
e a temperatura é necessário termos uma equação matemática adequada que nos
permita tal relação e a equação de
estado de um gás P.V = nRT
é ideal:
- P – pressão parcial dos gases no equilíbrio;
- V – volume da mistura gasosa em equilíbrio;
- n – número de moles do gás;
- R – constante universal dos gases.
Assim, a partir da
equação de estado de um gás podemos escrever:
P.V = nRT
A seguir consideremos a
seguinte equação da reacção:
N2(g) + 3H2(g)
⇌ 2NH3(g)
Imaginemos que temos num
recipiente fechado à temperatura e volume constante, o Nitrogénio (N2),
Hidrogénio (H2) e Amoníaco ou amónia (NH3) em equilíbrio.
Deste modo podemos dizer por exemplo, que pressão parcial do Hidrogénio é a pressão
que o Hidrogénio exerceria dentro desse recipiente se estivesse sozinho
ocupando todo o recipiente.
Deste modo podemos a
partir da pressão parcial de cada um dos gases expressar a concentração em
função da pressão, R e T:
P.V = nRT
Se formos a prestar
atenção podemos ver que determinamos as concentraçãoes de N2, H2
e NH3.
E agora vamos escrever a expressão
da constante de equilíbrio para a reacção:
Como já temos as
concentrações de todas as espécies podemos substituir na expressão de kc:
No denominador podemos
fazer a multiplicação dessas fracções: Lembre-se que na multiplicação de fracções,
os numeradores multiplicam-se entre si e os denominadores também:
Agora
temos a divisão de duas fracções e como sabemos na divisão de fracções,
mantém-se o numerador e multiplica-se pelo inverso do denominador:
No
denominador, aplicámos a propriedade comutativa (a posição dos factores não
altera o produto [resultado da multiplicaçao] ).
Assim
vemos que temos (RT)4 / (RT)2, portanto, temos a divisão de potências com a mesma base
porém com expoentes diferentes, pelo que aplicaremos a seguinte propriedade da
potenciação:
Agora
percebam que a relação:
é
exactamante o Kp:
Assim
podemos escrever:
Contudo
podemos reescrever a equação acima de outra maneira de modo a evidenciarmos um
aspecto importante:
Ao
reescrevermos esta expressão desta maneira queremos realçar que o expente -2
que vemos aí é nada mais e nada menos que a diferença entre o número de moles
dos produtos e reagentes (∆n):
Observe:
1N2(g) + 3H2(g)
⇌ 2NH3(g)
∆n
= nprodutos - nreagentes
∆n
= 2 – ( 1 + 3 )
∆n
= -2
Portanto,
a equação que acabamos de deduzir expressa a relação entre Kc e Kp sendo
definida em termos de Kc:
Assim,
de um modo geral podemos escrever que:















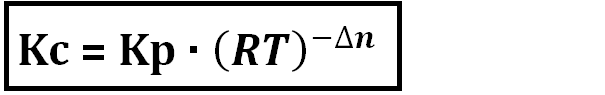





0 Comentários